人は「見方」を変えるのが嫌い
これまで「学習科学」という新しい研究分野を概観してきた。今回からはしばらく、人の考え方の特徴、あるいは人特有の「くせ」についてお話していきたい。考え方や問題の解き方に見られるくせだから、認知的「くせ」、と呼ぶことにしよう。教員も生徒も人だから、どちらも同じような認知的「くせ」を持っている。そういうものだと思っておくと、何かの折に役に立つかもしれない。
人はある一定の角度からものを「見て」、自分でこうだと思うと、もう世の中にはその見方しかないような気になってしまうことがある。このことを「肝に銘じて」いるかいないか、が、人の賢さを随分左右する。
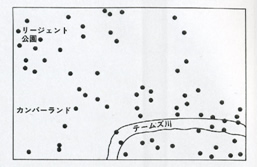
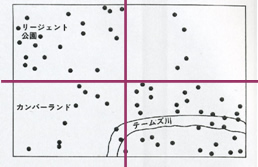
図1をみていただきたい。第二次世界大戦も終わりに近かったころ、ドイツが闇雲にロンドンに向けて撃っていた砲弾が、この図のような散らばり方で着弾している、というニュースが広がった。人々の間に、「リージェント公園があぶない」「いや、テムズ川付近がこわい」「あそこには連合軍の隠し倉庫があるらしい」、といううわさがどこまで広がったか正確には知らないのだが、とにかくこの図を見ると、当時のロンドンにいた人たちがそう思ったとしても無理はない。実際この図を図2のように4つに分割してみると、上のようなうわさには根拠があるようにすら見える。
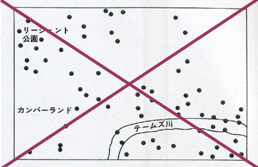
ところがこの図に、図3のような区切りを入れてみると、あら不思議、どこの三角形の着弾数が多いって??
この話の不思議なところは、なぜ人は、ロケット弾の着弾点にある特定のパタンがあると思い込んでしまうのか、というところだろう。人は、図1のような図があれば、自然にそれを図2のように、縦横に区切ってしまう。あるいは、文字があるところに目をつけてしまうと、左上、右下にたくさんの点が集まっているように見える。いったんそう見え始めたら最後、図3のような「反論」を思いつくのは、至難のわざである。この認知的「くせ」に対して身を守るとしたら、何かいいアイディアが湧いたら即、「他の見方はないか?」と考える「カウンターくせ」のようなものを身につける、といったようなことだろう。ただこれは、表だってやりすぎると「天邪鬼」に見える。
今見たような認知的「くせ」は、人も持つもう一つの認知的「くせ」と深く結びついている。人は、もともとばらばらなものに対してもある種の「パタン」を見て取ってしまう、というくせを持っている。特に意味のないデータから、無理やり推論してもっともらしい「仮説」を作り出すのが案外得意なのである。むしろ、「仮説が立たない」と不安になる。先の図で「テムズ川はあぶない!」と考えるのも一つの仮説である。「どこに向けて打ってくるのかわからない」より、「デムズ川沿いのなんらかの目標に向けて打っている」と考えたほうがわかりやすくて気が休まる。対処もしやすい。そういう「仮説」が見つかったのなら、それ以外のことは「考えないほうが良い。」だから、くせになる、のである。
困ったことに、人は仮説をさっさと作る割には、その正しさをちゃんと確かめるのが苦手である。中でも特に人は、自分自身の仮説を支持する証拠だけを探そうとして、仮説が間違っているかどうかをわざわざ確かめようとはしないという強い傾向を持っている。
このことを示す例として、次のような実験がある。実験に参加した人は、3つの数字のつながりを提示され、「この3つの数字はある規則にしたがって並んでいます。その規則を見つけてください」と教示される。どうやるか、というと、まず参加者は自分で3つの数字のつながりを作り出し、実験者に告げる。と、そのたびに実験者は、そのつながりが実験者の考えている規則に合っているかどうかを教えてくれる。これを何回か繰り返して参加者が規則を見つけたと思ったら、参加者はその規則を答える。規則が合っていれば、参加者の勝ち、である。
この実験で実験者が「3つの数字は、単に小さいものから大きいものへ、順に並んでいる」という、すごく簡単な規則を持っていて、実験に参加してくれた一人に対して「2-4-6」という3つの数字のつながりを提示したとしよう。この時、どんなことが起きるかをちょっと再現してみよう。
| 参加者 | : | (「実験者が考えているのは、「好きな数で始めて2ずつ足す」という規則ではないかと考えて、それに合う例を作り出す) 「8-10-12はどう」? 実験者:「その数の並びは、私の考える規則に合っています」 |
| 参加者 | : | (うれしくなって、もう一つ仮説に合う例を作ってみる) 「じゃ、14-16-18なら?」 |
| 実験者 | : | 「その数の並びは、私の考える規則に合っています」 |
| 参加者 | : | (もっとうれしくなったので、でも少し慎重にもっと小さい数から始めるものも試してみることにする)「じゃ、ああ、1-3-5だったら?」 |
| 実験者 | : | 「その数の並びは、私の考える規則に合っています」 |
| 参加者 | : | 「わかったわ!あなたの規則は、『好きな数に2ずつ足す』のでしょ!」 |
| 実験者 | : | 「いいえ」 |
| 参加者 | : | 「なんで?え、どして違うの?うそでしょ、いじわる!」 |
このあと、こんなやり取りが、延々と続く。ここで問題にしたいのは、規則が簡単だと見つかりにくいとかそういうことではなくて、人がどんなやり方で規則を見つけようとするか、である。この実験の参加者は、だれでも、それほど苦労せずに一つや二つの規則を思いつくことができる。しかし、仮説を作るとほぼ必ず、この例のように、その仮説に合う数のつながりを作って仮説を確かめようとする。疑り深く、「じゃあ、私の仮説には合わないんだけれど、1-2-3ってことはない、でしょうね?」と一度確かめさえすれば、「それも合ってるよ」と言われるので、そこで自分のあやまりにすぐ気付くはずなのだけれど、そういう確かめ方をする人は、ごくまれ、であることがわかっている。
この傾向は、科学者の世界でもしょっちゅう起きている。ガリレオが地動説を説明するために望遠鏡で木星を捕らえて、反対派の人たちに木星の周りを星が回っていることを見て確認するよう求めた時、天動説を信奉する反対派の幾人かは、そもそも望遠鏡をのぞいてみることそのものを拒否したという。仮説を反証することは、何が正しいのかを決めようとするとき仮説を支持することよりも一般に役に立つがわかっていても、人はなかなか自分の仮説を自分で否定するような考え方をしたがらない。
どうしたらいいのだろう?私たちは、いつでも、すごく意識して、「私の仮説は間違っているかもしれない、間違っているかもしれない、間違っているかもしれない」と3度は唱えるくらいにして、ちょうど良いくらい、頑固なものなのだ。先にも言ったように、この頑固さに自分ひとりで打ち勝つには、「人は思った以上に頑固だから、気をつけないと・・・」と自分に唱え続けるくらいしか、いまのところは対策がない。
ただここで、なにも自分ひとりで戦わなくてもいいじゃないか、と思えるなら、話は大分変わってくる。他人は、あなたの仮説を必ずしも知っているわけではないので、例えば二人の参加者が上のゲームを一人ずつ交代しながらやるとすると、それぞれが勝手に自分の仮説に「合う」3つの数字を考えたとしても、二人の仮説が違えば当然、一人の仮説はもう一人の仮説には「合わない」可能性が高くなる。このゲームだと、他人の考えていることが、3つの数字の列という互いに「見える」形で提示されるので、自分の仮説に合わないテストが行われるチャンスも多くなる。科学の世界では研究者が共同で仮説の検証にあたることが多くなってきているが、共同作業のメリットは、こういうところにもあるのだろう。
図版出典:ギロビッチ、1993、『人間この信じやすきもの』、新曜社、p. 32.