国語 だれがたべたのでしょう(小学校1年生で実施)
説明文『だれがたべたのでしょう』に出てくる「松ぼっくりとリス」、「木の葉とむささび」のそれぞれのエピソードを読んだ子どもがペアを組み、「このお話では、食べたあとを見ると、どんなことがわかると書いていますか」という課題のこたえを教科書の中に探します。
ジグソー課題
このおはなしでは、たべあとをみると、どんなことがわかるとかいていますか。
エキスパート
エキスパートA:「だれがまつぼっくりを食べたのか」の読み取り
エキスパートB:「だれが木の葉を食べたのか」の読み取り
エキスパートB:「だれが木の葉を食べたのか」の読み取り
期待する解答の要素
穴の開いたクルミの殻や芯だけになったまつぼっくり、ちぎれた木の葉など食べたあとをよくみると、どんな動物が暮らしているのかが分かる。
ポイント
小学校低学年で実施した例です。同じ構造が繰り返し出てくる説明文の中で、「問い」と「答え」の呼応した関係をつかんでいくことをねらいます。エキスパート活動に入る前に、全員で「だれがクルミを食べたのか」をワークシートを用いて読み取っておくことによって、子どもたちもその後の活動のイメージがつきやすくなります。
国語 大造じいさんとがん(小学校5年生で実施)
「大造じいさんの言動」「残雪の行動」「情景描写」に注目して大造じいさんの心情をそれぞれ読み取った子どもたちが、「大造じいさんは、なぜ残雪を放したのだろう」という問いについて考えます。
ジグソー課題
大造じいさんは、なぜ、残雪を放したのだろう。
エキスパート
エキスパートA:大造じいさんの言動
エキスパートB:残雪の行動
エキスパートC:情景描写
エキスパートB:残雪の行動
エキスパートC:情景描写
期待する解答の要素
①大造じいさんの心情 ②残雪のとった行動 の2つの視点から、大造じいさんの人間性や生き方・考え方を含めた内容
例)威厳のある残雪の姿に強く心を打たれ、英雄である残雪と正々堂々と戦いたいと思ったから。
例)残雪をただの鳥ではなく、自分と対等な生き物だと考えているから。
例)威厳のある残雪の姿に強く心を打たれ、英雄である残雪と正々堂々と戦いたいと思ったから。
例)残雪をただの鳥ではなく、自分と対等な生き物だと考えているから。
ポイント
単元全体を通してジグソー法の授業を展開した例です。「大造じいさんとがん」のテクストを(1)「うなぎつりばり作戦」、(2)「たにしばらまき作戦」、(3)「おとりがん作戦」、(4)「残雪を放した大造じいさん」の4場面に分け、各場面で「大造じいさんの言動」「残雪の行動」「情景描写」のエキスパートに分かれ、それぞれの叙述から大造じいさんの心情を読み取っていき、最終的にメインの課題の答えを考えます。場面ごとに各エキスパートの担当者を入れ替えることで、単元を通じて必ずどのエキスパートも一度は経験できるようにしているのも教材作成者の工夫です。
社会 森林を守る取り組み(小学校5年生で実施)
「森林の手入れ」、「林業の後継者がいない」、「輸入材が使われる」という林業をめぐる問題に関する知識を持ち寄って、「木を使うことがどうして森林を守ることになるのか」という問いについて考察します。
ジグソー課題
木を使うことが、どうして森林を守ることになるのか。
エキスパート
エキスパートA:森林の手入れ(手入れされない森林はすぐにあれる)
エキスパートB:林業の後継者問題(高齢化が進んでいる)
エキスパートC:国産材と輸入材(安い輸入材が消費されている)
エキスパートB:林業の後継者問題(高齢化が進んでいる)
エキスパートC:国産材と輸入材(安い輸入材が消費されている)
期待する解答の要素
安い輸入材ではなく国産材を使うことが、林業で働く人々の仕事を増やすことになる。林業が盛んになれば、あれた森林にはならず、森林を守ることへとつながっていく。
ポイント
林業体験で子どもたちが実際に得た知識をエキスパート資料の中に盛り込んで、単元の中で体験活動との連続性を持たせたデザインになっています。子どもたちにとって、それぞれのエキスパート活動で得られた知識だけですぐにジグソー課題の答えが出るわけでないので、3つの知識を組み合わせる過程で、疑問を持ってそれぞれの知識を確認したり、何度も聞きなおしたりするような学びの姿がみられたとの授業者のコメントがありました。
算数 九九をつくろう(小学校2年生で実施)
複雑な形に並んだものの個数を求めるために、「2つに分けてそれぞれ掛算で求めたものを加える」、「一部を移動させて掛算で求める」、「空いているところを埋めて掛算で求める」という3つの方法をそれぞれ学んだ子どもたちが集まって、九九を利用したものの数え方を工夫します。
ジグソー課題
箱の中のチョコレートは全部で何個ありますか?


エキスパート
エキスパートA:分けて考える
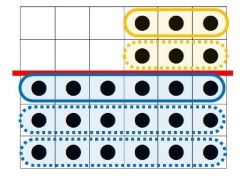 エキスパートB:移動して考える
エキスパートB:移動して考える
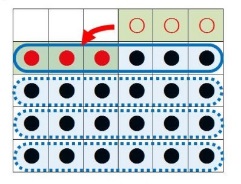
 エキスパートB:移動して考える
エキスパートB:移動して考える
エキスパートC:あいているところを埋めて考える
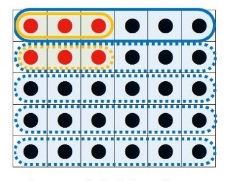
期待する解答の要素
複雑に並んだものの数でも,分割・移動・補完することによって,いくつのまとまりがいくつ分あるかがとらえやすい形(長方形)にすると、乗法九九を使って個数を求めることができる。
確かめ課題
箱の中のチョコレートは全部で何個ありますか?






ポイント
乗法の意味をつかむことに焦点を当てることで、多様な学びを許容できるふところの深い教材になっています。なんとなく個数がわかるところから「まとまり」を意識できるところへ、一種類の考え方で「まとまり」をみつけられるところから、分割・移動・補完を駆使して様々な「まとまり」をみつけられるところへ、授業をとおして児童にはそれぞれ深まりがありました。
算数 複合図形(小学校4年生で実施)
長方形を組み合わせたL字型の面積の3つの求め方について、「計算を見てその意味を言葉で説明する」活動に取り組んだ子どもたちが集まって、3つの方法の特徴を表す名前を考え、方法を比較して複合図形の求め方のコツをまとめます。更に、コツを活用して、四角ドーナツ型と直角三角形の面積を求めるという発展課題に取り組みます。
ジグソー課題
右図のような形の面積を求める方法を4人の人が考えました。それぞれの考え方(式)にふさわしい名前をつけて、複合図形の面積の求め方のコツをキーワードでまとめましょう。
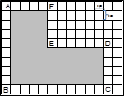

エキスパート
エキスパートA(導入で確認):8×4=32、4×6=24、32+24=56
 エキスパートB:8×10=80、4×6=24、80-24=56
エキスパートB:8×10=80、4×6=24、80-24=56
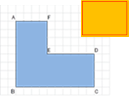 エキスパートC:8×(10+4)=8×14=112、112÷2=56
エキスパートC:8×(10+4)=8×14=112、112÷2=56
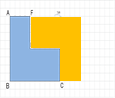
 エキスパートB:8×10=80、4×6=24、80-24=56
エキスパートB:8×10=80、4×6=24、80-24=56 エキスパートC:8×(10+4)=8×14=112、112÷2=56
エキスパートC:8×(10+4)=8×14=112、112÷2=56
エキスパートD: 8×(4+3)=8×7=56
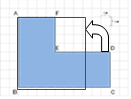
期待する解答の要素
長方形(これまでに学習した図形)をみつけて、足したり、引いたり、2で割ったりすれば、求められる。
発展課題
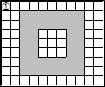
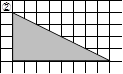 左の図形の面積を求める
左の図形の面積を求めるポイント
習った計算式を使って答えを出すだけでなく、既習事項を使って見たことのない図形の面積の求め方を見出す、そんな探究的で創造的な学びを引き出すために丁寧に工夫された教材です。授業の最初に、授業前に多くの子どもが気づくことができた「分ける」考え方(エキスパートA)に全員で名前をつけ、活動のイメージをつかませたことで、児童が見通しを持って活動にとりくめました。学習をとおしてほとんどの子どもたちが、発展問題のドーナツ型や三角形の面積を求めるための2種類以上の方法を思いつくことができました。
理科 流れる水のはたらき(小学校5年生で実施)
流れる水の浸食作用、川のカーブの内側と外側の流れの速さの違い、流れの速さと運搬作用・堆積作用の関係について学んだ子どもたちが集まり、川が大きく曲がったのはなぜかを考えます。
ジグソー課題
どうして写真のように川が曲がったのかを考えよう
エキスパート
エキスパートA:流れる水によって地面が削られる様子の観察
エキスパートB:川のカーブの内側と外側の流れの速さの違いの観察
エキスパートC:流れる水によって土や石が流されること、積もることの観察
エキスパートB:川のカーブの内側と外側の流れの速さの違いの観察
エキスパートC:流れる水によって土や石が流されること、積もることの観察
期待する解答の要素
川のカーブの内側は流れが遅く、外側は流れが速いため、外側のかべは流れる水のはたらきでどんどん削られる一方、内側のかべには上流から流されてきた土や石などが積まれていく。これらの水のはたらきが続いていくことで、長い年月をかけて川のカーブが大きくなった。
ポイント
単元の導入においてこれからの学習のおおまかなイメージをつかませるところで、知識構成型ジグソー法を活用した実践例です。エキスパートでは実験のビデオを素材として使いました。子どもたちは堆積・運搬・浸食という流れる水のはたらきを、映像や課題として提示された具体例と結び付けながら自分なりの言葉でつかみました。この時点で語れるようになったことは誤った部分もありましたが、この時間で培ったイメージは、先生や教科書の解説を理解していくための基礎になり、以後の学習が効率的に進みました。

