人は自分でこうだと思ったものに足をすくわれることがある。このことを「肝に銘じて」いるかいないか、が、人の賢さを左右する。
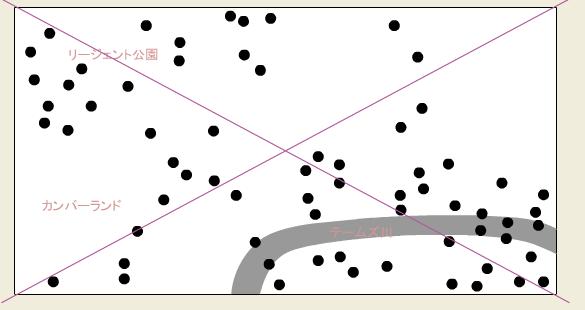
図1をご覧下さい。第二次世界大戦も終わり近く、ロンドンで観察されたドイツ砲の着弾地点図である。人々の間に、「リージェント公園があぶない」「いや、テムズ川付近がこわい」「あそこは連合軍の隠し倉庫があるらしい」など、うわさが広まった。ところが図2のような区切りを入れてみると、あら不思議、どこの三角形の着弾数が多いって??
図1 ロンドン中心部に落ちた67発のV-1ロケット着弾箇所

図1を見ると、どうしたって左上と右下にたくさんの点が集まっているように見える。いったんそう見え始めたら最後、図2のような「反論」を思いつくのは、至難のわざである。これは科学者でも難しい。
科学者は、データからパタンを見つけ「仮説」を作り出す。「テムズ川はあぶない!」と考えるのも一つの仮説である。仮説を作ることそのものは実はそれほど難しくない。難しいのは、自分自身の仮説が間違っているかどうかをきちんと確かめることで、人はこれがなかなかうまくできない。
図2 ロンドン中心部に落ちた67発のV-1ロケット着弾箇所
このことを示す例として、次のような実験がある。課題は、2-4-6という 3つの数字のつながりを提示され、「この3つの数字はある<規則>にしたがって並んでいます。その規則を見つけなさい」というものである。回答者は、自分で3つの数字のつながりを作って実験者に告げる。と、そのたびに実験者は、そのつながりが<規則>に合うかどうかを教えてくれる。これを繰り返して規則を見つけたと思ったら、回答者はその規則を答える。規則が合っていれば、回答者の勝ち、である。
今、<規則>が、「3つの数字は、小さいものから大きいものへ順に並んでいる」という、すごく簡単なものだったとしよう。この時、起きそうな会話を再現してみると、
|
回答者:(<規則>は、「2ずつ足す」のだろうと考えて)「8-10-12」 実験者:「その数の並びは、私の考える規則に合っています」 回答者:(うれしくなって)「じゃ、14-16-18」 実験者:「その数の並びは、私の考える規則に合っています」 回答者:(もっとうれしくなったので、少し慎重に)「じゃ、ああ、1-3-5は?」 実験者:「その数の並びは、私の考える規則に合っています」 回答者:「わかったわ!あなたの規則は、『2ずつ足す』でしょ!」 実験者:「いいえ」 回答者:「なんで?え、何で違うの?うそでしょ、いじわる!」 |
普通、こんなやり取りが、延々と続く。途中で、一回でもいいから、疑り深く「じゃあ、私の仮説には合わないんだけれど、1-2-3ってことはない、でしょうね?」と確かめさえすれば、「それも合ってるよ」と言われてすぐ自分のあやまりに気付けるはずなのだけれど、そういう確かめ方をする人は、ごくまれである。
ガリレオが地動説の証拠として木星の周りを星が回っていることを見せようとした時、反対派の幾人かは、そもそも望遠鏡をのぞいてみることそのものを拒否したという。人は、科学者であってさえも、なかなか自分の仮説を自分で否定するような考え方をしたがらない頑固者である。「人は思った以上に頑固だから、気をつけないと・・・」といつでも自分に言い聞かせるくらいで、ちょうど良さそう、である。

