話し合いで自分の殻を破る

　ここ数回、人がものを考える時、客観的に考えるのは案外難しいという話しを繰り返ししてきた。人は、これまで経験してきたことや自分が良く知っていること、あるいは今自分の興味のあることなどをよりどころにものを考える。「よりどころに」という言い方を否定的に言うと、引きずられてしまうということになる。認知研究分野での専門用語ではこのよりどころに偏ることを「認知的偏り（認知的バイアス）」と呼ぶのだが、では、それから自由になるにはどうしたらいいのだろう？これまでの解説では、｢まぁ、人はそういうものですので、そのことをできるだけ自覚して、何か考える時はいつでも自分が偏っている可能性があることを自問してみたらどうでしょう？」というような言い方でお茶を濁してきたのだが、認知研究の中からもう少し積極的な対処方法を見つけることができてもよさそうである。今回は、この自分の考え方の殻をやぶるために役に立つかもしれない方法について話をしたい。

拍子抜けされるかもしれないが、自分の考えにとらわれないためにおそらく最も手軽に実行できて、しかもかなり効果があることが知られているのは、｢他人とまじめに話し合う｣ことである。学習科学では、この一見簡単なことに見える｢他人と話し合う｣という活動を、協調的学習活動というような呼び方をして、いろいろ研究している。

例えば、複数の人で同じ問題を話し合いながら解く協調的な問題解決過程についての研究の成果としては、

1. 人がふたり以上いると、他人が自分ひとりでは気付かなかった見方を提供してくれることがあり、
2. その他人の見方をうまく自分の考え方と比較対照吟味できると
3. 自分でいままでわかっていたと思っていたことをもっと深く考え直すきっかけができて
4. その結果、話し合う前よりも理解が深まることがある

ということになっている。一般にふたりで考える方がひとりで考えるより手間も時間もかかるのだが、その分、その場にでてくるさまざまな見方を突き合わせて全体として整合的な考え方を求める活動が自然に起きて、ひとりひとりの考え方が前より深くなる傾向がある。途中でいい答えが出たと思っても、相手がすぐには納得しないので、説明し続けているうちにまた自分で自分の説明に穴を見つけたりすることも多いので、問題に取り組む動機付けも増す。

こういう利点は、協調的な活動をするひとりひとりが自分なりの考えを持っている時の方が働きやすいが、相手が何も知らなくても起きることがある。良く分かっていない方が頑固にわからないと言い続けると、わかっている方の説明意欲がどんどん増すというようなこともないではない。うまい協調的問題解決活動が起きるかどうか、は、場面の設計次第でもある。

話しがちょっと抽象的になってきたので、計算を題材にした具体例を出してみよう。大学生に折り紙を渡してその｢4分の3の3分の2に色を塗る（実際の実験の時には簡単のためにその部分にざっと粗い斜線を引いてもらう）｣ことを求めると、大抵人は折ったり目盛をつけたりして折り紙の上に直接答えを出す。計算して(やってみると答えは2分の1になる)、それから渡された折り紙を2等分して片方だけ斜線を引いてもよいのだが、最初から計算する人は1割もいない。さらに、この直後に別の折り紙を渡して今度は「3分の2の4分の3に斜線を引く」ように頼んでも、2度目も折るなどして答える人がほとんどである。と、ここまでは、一人でやってもらう時の話である。

これに対して2人一組のペアを作って、その人たちに同じことを頼むと（この時、折り紙は二人に一枚、鉛筆も二人に一本しか渡さない）、最初の問題では一人の時とたいしてやることが変わらないが、2度目には7割の組が計算する。つまり、この場合、協調的に問題を解く過程を経験することによって、7割の人たちが「どちらの問題も計算で解ける」こと、つまり一般解が存在することに気付いてそれを使うようになる。

図1：ペアで起きていること

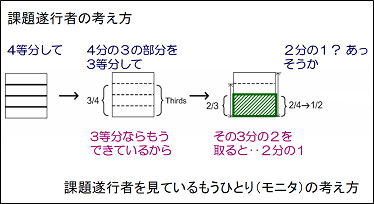
「4分の3の3分の2」を求める問題を解く時、2人組で何が起きるのかをビデオに撮って詳しく見てみると、典型的にはまず1人の学生が折り紙を4等分し、せっかく折ったものを開いて、その「4分の3」の部分をさらに別の折り方をして3等分しようとする。図1に一つ例を出したが、それを見てもらうとわかるように、4等分の4分の3の部分はすでに3等分されているので、それまでに付いた折り目を利用するなどすればさらに3つに折る必要はない。しかし、折って答えを出そうとしている本人は、たいていの場合そのことに気付いていない。それに気付いて「3等分ならもうできているんじゃないの？」などの発言をするのは、そこまで見ていたもう1人の学生であることが多い（分析した9組の内7組、78％がこのケースに当たった）。言い換えると、折り紙を折って課題を解いている本人(課題遂行者と呼ぼう)は、いわば自分の解き方に｢囚われていて｣そのやり方一本で行こうとするのに対して、それを見ているもう一人は、なにしろ自分でやっていないのである意味余裕があるのか全体に目配りを利かせやすいらしい。二人で問題を解くということは、こんなふうに少しずれたものの見方がぶつかり合うことでもあって、そのために、一人が自分のやり方に囚われるのを防ぐ働きをするらしい。

もう少しこの話を続けると、これも上の図1を見るとわかるように、｢すでに3等分されているものの3分の2に色を塗る｣とその結果、色が塗られた部分は折り紙全体の2分の1になる。この問題を一人で解いていると、大学生でもこのことに気付かない場合が少なくない。その証拠に、2分の1に色を塗った学生に｢答えはどうなりましたか？｣という聞き方をすると、縫った部分を手で指して、「ここ」という学生が多い。中には、自分が色を縫った折り紙をじっと見直して｢答えって・・・2分の1ですか？｣という学生もいないことはないのだが、そういう学生はそもそも少ないし、その行動を見ていると、ある種の気付きなおしを経て始めて2分の1が見えているらしい。

ふたり組みの学生では頻繁にこのような見立て直しが起きる。その結果、話し合っているうちに、｢ならこの問題は最初から計算しても解ける｣というようなことを言い出して、他の問題にも一般化可能な解法に気づく。そこに2問目が来ると、じゃ、今度は計算してしまえ、ということになりやすいのだと思われる。つまり、協調的な問題解決場面は、参加者を自然に課題解決者とモニターとに分け、モニターは問題解決者の解法を「見て解釈」せざるを得ない立場に置かれるため、その場に「少しだけ抽象的な」解釈を持ち込む役割を果たす。この課題遂行役とモニター役が頻繁に入れ替わり、複数の解法が、少しずつ抽象度を上げて生み出される。一人ひとりの学生はそれらの解を統合しようと努力する結果、それぞれのレベルに応じて、一人の時よりは一般的な解を掴みやすくなるのだと考えられる。

　科学の最先端で研究を進める科学者たちも、こういう理解深化をひきだすような協調作業を日々行っている。学生もいずれはこういう現場で知的な生産作業に関わるようになることを考えると、学校での授業を通してこういう知的な協調作業の体験ができることにはメリットがありそうである。